平均値(アベレージ)について
平均値は全データの中で真ん中の値になり、平均値と比較することでそのデータ全体に対して、どのレベルであるかを判断することができます。
ただし、平均値は極端なデータに影響されるため、数個のデータがと極端に大きい数値の場合に、大半が平均以下になるようなこともあります。
※その逆で数個のデータが極端に小さい数値で、大半が平均以上になることもあります。
全体の傾向を見ることができのが平均値。
ただし、極端なデータに影響を受ける値である。
平均値の求め方
平均値は各データの値の総和をデータの個数で割って求めることができます。
以下のようなデータがあった場合は、10個のデータの総和÷10で求めることができます。

(100+100+130+130+150+140+130+100+900+1000)÷10=288
Excelの場合はAverage関数で求まることができます。
中央値(メジアン)とは
中央値は、データの集まりのちょうど中央になる値のことをいいます。
平均値は極端なデータの影響を大きく受けるのに対して、中央値は極端なデータの影響を受けにくく、真ん中の値を知ることができます。
データの真ん中の値が中央値です。
極端なデータに影響を受けにくく、真ん中の値を知ることができます。
中央値はデータを大きさ順に並べて真ん中の値となり、それ以外のデータ・データの全体像を考慮した値ではないため、極端なデータの場合は、中央値とほとんどのデータが離れてしまうことがある。
中央値を見るときは、最小値や最大値も調べて、最小値、最大値に対して中央値を考えることで全体像が見えやすくなります。
中央値の求め方
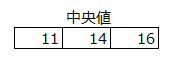
データの個数が奇数の場合は、真ん中のデータが中央値になります。以下の例の場合は、14が中央値になります。
データの個数が偶数の場合は、大きさ順に並び替えて中央に隣接するデータの平均が中央値になります。以下の例の場合は、6.5が中央値になります。

Excelには中央値を求めるための関数として、MEDIANが用意されています。
Excelの場合は、MEDIAN(セル範囲)で中央値を求めることができます。
最頻値(モード)とは
最頻値はデータの中で最も頻繁にでてくる(頻度の高い)値のことです。
データが度数分布で与えられている場合は、度数の最も大きい階級の値を最頻値とします。
最頻値は中央値と同様に極端なデータに左右されにくいメリットがあります。
デメリットとしては、データの値が少なすぎる場合はあまり効果がないことです。
最頻値の求め方
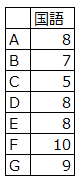
最頻値は最も頻繁にでてくる値ですので、以下表の場合は8が最頻値になります。
ExcelのMODE関数を使って、MODE(セル範囲)で最頻値を求めることができます。