本記事では、データベーススペシャリストの試験対策として、非正規形から第1正規形、第2正規形、第3正規形までの正規化をわかりやすく解説します。
私のように正規化が苦手な方も多いと思いますので、試験対策に役立てていただけたら幸いです。
- 正規化(Normalization)とは
- 正規化の目的
- 正規形の種類
- 非正規形について
- 第1正規形について 非正規形から第1正規形に正規化する
- 候補キー、主キーの決定
- 第2正規形について 第1正規形から第2正規形に正規化する
- 第3正規形について 第2正規形から第3正規形への正規化
正規化(Normalization)とは
一定のルールに基づいて加工することを言います。
データベースでは、「正規化理論」(一定のルール)に基づいて、データの構造を整理して、重複や矛盾をなくすことです。
正規化の目的
正規化する目的は以下の通りです。
・関係データベースでタプルの挿入・更新・削除時に起こる更新時異常を排除すること。
・一貫性、整合性を確保しながら、データの冗長性(無駄な部分)を排除し、独立性を高めること。
・1ヵ所1事実(1 fact in 1 place)を実現し、更新時異常を発生しないようにすること。
正規形の種類
正規化できるリレーションを正規形といいます。
第1正規形から第5正規形まで、6種類の正規形があります。
非正規形はまだ正規化をしていないリレーションです。
・非正規形
↓正規化
・第1正規形
↓正規化
・第2正規形
↓正規化
・第3正規形
↓正規化
・ボイスコッド正規形
↓正規化
・第4正規形
↓正規化
・第5正規形
非正規形について
非正規形の定義は、リレーションの属性値の中に単一でない値が含まれていることです。
本記事では以下画像をもとに解説します。顧客名(顧客番号)が、単一値ではなく顧客名、顧客番号と複数の値が入っているため、非正規形と分かります。
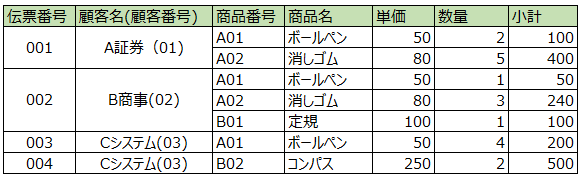
第1正規形について 非正規形から第1正規形に正規化する
第1正規形の定義は、リレーションRの属性値がすべて単一値であることです。
非正規形から第1正規形に正規化するためには、直積集合やべき集合を排除して、属性値がすべて単一値となるように加工します。
直積集合の排除
直積集合とは、各集合を組にしたのもので、以下の画像では「顧客名(顧客番号)」が直積集合にあたります。
1つのドメイン(1マス)に複数の値が入っていてるため、単一値となるように「顧客名」、「顧客番号」を別属性に分けて、直積集合を排除します。

べき集合の排除
べき集合は、「すべての部分集合の集合」のことです。
今回の場合では、1つの伝票番号に複数の商品番号が紐づいているように、1つの値に複数の値(集合)が対応していることを意味します。
例:伝票番号001に商品番号A01、A02が紐づいている。
1つの値に1つの値を対応させて、べき集合後排除します。

直積集合、べき集合を排除することで、属性値がすべて単一値となり、第1正規形への正規化が完了します。
■第1正規形のテーブル構造
伝票(伝票番号,顧客番号,顧客名,商品番号,商品名,単価,数量,小計)
第1正規形のポイント
・第1正規形は、すべての属性値が単一値となること
・非正規形から第1正規形への正規化は、直積集合、べき集合を排除する (繰り返し項目をなくす)
候補キー、主キーの決定
第1正規形から第2正規形に正規化する前に、リレーションの候補キー、主キーを決定します。
候補キー (CANDIDATE KEY)
候補キーの定義は、リレーションのタプルを(行)を一意に識別できる属性または属性の組のうち、極小であるものです。
極小とは余分な属性を含まない、必要最小限の組み合わせを言います。
主キーとは異なり、候補キーはNULLを許可する属性をもつ(または含む)ものでも可です。

※顧客は複数買い注文するため、伝票番号は複数存在する
※顧客番号と顧客名、商品番号と商品名は1対1である
以下の順番で候補キーを考えます。
①リレーションのタプルを一意に識別できる属性または属性の組み合わせ を考える
②その中で極小のもの を考える
①を満たす属性または属性の組み合わせを考えると、かなりたくさんの組み合わせが考えられます。
{伝票番号,顧客番号,顧客名,商品番号,商品名,単価,数量,小計}
{伝票番号,顧客番号,顧客名,商品番号,商品名,単価,数量}
{伝票番号,顧客番号,顧客名,商品番号,商品名,単価}
:
:
次に①の中で極小のものを考えます。
{伝票番号,商品番号}の両方が重複するタプルは存在しない、かつ、伝票番号、商品番号のどちらか1つではタプルを一意に識別できません。これ以上属性を減らすことができない『極小』のものとなります。そのため、{伝票番号,商品番号}が候補キーとなります。
また、{伝票番号,商品名}も候補キーとなります。
※候補キーは1つとは限りません。
主キー (PRIMARY KEY)
主キーは、候補キーの中から最もふさわしいものが選ばれます。
主キーは、一意性制約と非NULL制約を併せ持ちます。
今回は、{伝票番号,商品名}を主キーとします。
第2正規形について 第1正規形から第2正規形に正規化する
第2正規形の定義は次の通りです。
<第2正規形の定義>
リレーションRが次の2つの条件を満たすこと。
・Rが第1正規形であること
・Rのすべての非キー属性は、いかなる候補キーにも部分関数従属していないこと (完全関数従属していること)
※候補キーが単一キーの場合は、すでに第2正規形の定義を満たしています。
候補キーが複合キーの場合のみ、第2正規形の定義を満たしているかどうかを判断する必要があります。
完全関数従属と部分関数従属について
『完全関数従属』とは、①関数従属性 「候補キー:X → 非キー属性:Y」が成立するが、②「候補キー:Xの真部分集合 → 非キー属性:Y」が成立しないときの状態、性質のことです。
『部分関数従属』とは、①が成立し、②も成立・存在しているときの状態、性質のことです。
『部分関数従属』が存在すると、『完全関数従属』ではありません。
第1正規形から第2正規形への正規化では、『部分関数従属』を排除して『完全関数従属』とします。
『部分関数従属』の排除
第2正規形への正規化のために、部分関数従属がある場合は排除します。(部分関数従属を排除することで完全関数従属となる)
部分関数従属の排除は、候補キーに対して部分関数従属となっている関数従属性を別のリレーションに分解します。
『部分関数従属』の条件は以下の通りです。
①「候補キー:X → 非キー属性:Y」が成立する
②「候補キー:Xの真部分集合 → 非キー属性:Y」が成立する
伝票(伝票番号,顧客番号,顧客名,商品番号,商品名,単価,数量,小計)
主キー:{伝票番号,商品番号}
候補キー:{伝票番号,商品番号}、{伝票番号,商品名}
非キー属性:{顧客番号}、{顧客名}、{単価}、{数量}、{小計}
「①「候補キー:X → 非キー属性:Y」が成立する」を確認します。
「候補キー」から「非キー属性」を導くことができるので、①は成立していることが分かります。
{伝票番号,商品番号} → {顧客番号}、{顧客名}、{単価}、{数量}、{小計}
{伝票番号,商品名} → {顧客番号}、{顧客名}、{単価}、{数量}、{小計}

「②「候補キー:Xの真部分集合 → 非キー属性:Y」が成立する」を確認します。
「候補キー:Xの真部分集合」とは、候補キーの一部です。
{A,B,C}の真部分集合は、{A,B,C}を除く{A},{B},{C},{AB},{AC},{BC},{空集合}です。
②では候補キーの一部のキーから、非キー属性が導けるかどうかを確認します。
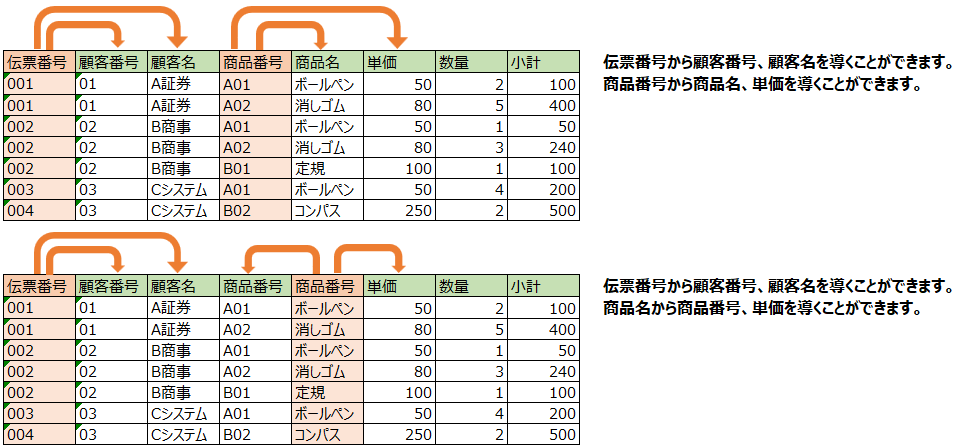
画像の通り、候補キーの新部分集合で非キー属性が導けることが分かります。つまり、部分関数従属性です。
{伝票番号}→{顧客番号,顧客名}
{商品番号}→{商品名,単価}
{商品名}→{商品番号,単価}
部分関数従属性の{伝票番号}→{顧客番号,顧客名}、{商品番号}→{商品名,単価}を別のリレーションに取り出します。

伝票明細{伝票番号,商品番号,数量,小計}
伝票{伝票番号,顧客番号,顧客名}
商品{商品番号,商品名,単価}
第2正規形のポイント
・候補キーの真部分集合(候補キーの一部)から決定される非キー属性がない状態
(非キー属性が候補キーの真部分集合に部分関数従属していない状態)
・第2正規形にするには、部分関数従属を排除する
・第1正規形の候補キーが単一キーであれば、すでに第2正規形である
第3正規形について 第2正規形から第3正規形への正規化
第3正規形の定義は次の通りです。
<第3正規形の定義>
リレーションRが次の2つの条件を満たすこと。
・Rが第2正規形であること
・Rのすべての非キー属性は、いかなる候補キーにも推移的関数従属していないこと
第2正規形から第3正規形への正規化は、第2正規形から推移的関数従属性を排除します。
推移的関数従属性とは
リレーションRの属性X,Y,Zにおいて、以下3つの条件を満たす場合、ZはXに推移的関数従属しています。
①X → Y
②Y → X でない
③Y → Z
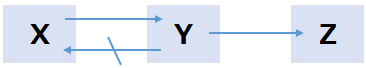
推移的関数従属性しているとき、次の2つが成立します。
ⅰ)X → Z
Ⅱ)Z → X でない
以下のリレーションで推移的関数従属性を考えます。
伝票{伝票番号,顧客番号,顧客名}
①{伝票番号} → {顧客番号} は成立します。
②{伝票番号} → {顧客番号} は成立しません。
※顧客番号03には、伝票番号003、004が導いており、一意の値を決定できない。
③{顧客番号} → {顧客名}は成立します。

顧客名は伝票番号に推移的関数従属しています。
推移的関数従属性の排除
第2正規形から第3正規形に正規化するために、推移的関数従属性を排除します。
X → Y → Z の関係において、Y → Zを別のリレーションに分けます。
そして、Yは元のリレーションにも外部キーとして残します。

導出属性の排除
導出属性は、小計(単価×数量)、消費税(小計×税率)、年齢(生年月日から算出)など、計算によって得られる属性のことです。
第3正規化に際し、導出属も排除します。

伝票明細{伝票番号,商品番号,数量}
伝票{伝票番号,顧客番号} ※顧客番号は顧客{顧客番号}の外部キーとなる
顧客{顧客番号,顧客名}
商品{商品番号,商品名,単価}
導出属性は多くの場合、候補キーに推移的関数従属していることが多く、推移的関数従属性を排除するタイミングでおのずと取り除かれる。
※すべての導出属性が候補キーに推移的関数従属しているわけではない。
「小計」について
{伝票番号,商品番号} → {商品番号,数量} → {小計}が成立し、かつ
{商品番号,数量} → {伝票番号,商品番号} が成立しないため、推移的関数従属しています。

本記事では、第3正規形への正規化までを取り扱うため、ボイスコッド正規形、第4正規形、第5正規形は扱いません。
以上、お読みいただきありがとうございました。